This thing got long and can basically be summarised as:
I factored smaller RSA numbers on free cloud computing using excellent open source software.Whats with the weird title?
"THE MAGIC WORDS ARE SQUEAMISH OSSIFRAGE"
is the plain text solution to many cryptographic challenges. I first saw it appear one character at a time from a CBC padding attack, and I started googling it. The origin of the sentence lie with a challenge set by the authors of the RSA encryption algorithm in 1977.
RSA was introduced to the world in this article in Scientific American in 1977 . In that article a message encrypted with a 129 decimal digit public key is given and an $100 prize is offered to anyone who can decrypt it.

At the time it was estimated that by the methods known at the time it would take millions of years to break. In fact thanks to advances in factoring algorithm and computing power it took only until 1994. A team successfully factored the 129 digit semi prime reconstructed the private key and decoded the text to reveal the sentence. Here is their announcement.
I have always found the basic proposition at the heart of RSA encryption hugely counter intuitive. How can it be that people much smarter than me using vast computer resources cannot find which two prime numbers I multiplied together when the product reaches 300 decimal digits?
What would it take to answer the 129 digit challenge that seemed near impossible in 1977. How difficult is the problem with modern factoring algorithms, software and cheap cloud computing?
The team that claimed the prize for what became known as RSA-129 used the Bonic framework to distribute the computing amongst volunteers. Apparently 1600 machines were used over a period of eight months. The algorithm used was the Multiple Polynomial Quadratic Sieve. It was considered the best understood factoring algorithm at the time.
Cado-nfs is an implementation of the number field sieve it is made up of several individual programs that will perform each of the steps necessary. I chose this implementation for a couple of reasons: Firstly it was written fairly recently and is maintained so the build dependancies are easy to satisfy. Secondly the D in it's title stands for distributed as it has been built with distribution across several servers in mind.
Coincidentally to this google offered a great free trial of 2 months and $300 of credit on their cloud platform. Which is a pretty good deal if you like playing around with CPU intensive stuff like me.
In order to give cado-nfs a spin I started up a high CPU instance on google's cloud compute engine and set it off with RSA-100 a 100 digit semi-prime first factored in 1991. On a single instance it took 148 minutes. or nearly 2.5 hours. This is quite impressive given that it took days across many more machines to achieve the original result admittedly using a slower sieving algorithm. Unfortunately (or fortunately for security) factoring times do not scale linearly with the moduls length. Before tackling anything longer I decided to try out cado-nfs distributed capabilities. Doing this couldn't really be easier. A master process uses SSH to start and control threads on slave machines which it allocates work over an HTTP API. All this is handled automagically all that you have to do is make sure the slave machine has the master's ssh key authorised and then start the master process with the ip-address of the slave machines.
Using this method I managed to get the time for RSA-100 down to 77 minutes across 2 machines and 47 minutes across 4 machines. I stopped at 4 machines or 8 CPUs as I hit the CPU limit for free instances on Googles platform. I later discovered that I could run 8 CPUs per region so with three regions I could use 24 CPUs in total on 12 virtual machines.
With four machines I felt my set up was probably good enough to tackle some longer problems. I factored RSA-110 and RSA-120 experimenting with parameters as I went.
Here are some times I found:
| CPU Time (s) | Elapsed Time (s) | CPU Time (hrs) | Elapsed Time (mins) | Machines | |
| RSA100 | 15466.6 | 8883.19 | 4.296277778 | 148.0531667 | 1x |
| RSA100 | 15213.6 | 4641.16 | 4.226 | 77.35266667 | 2 x |
| RSA110 | 55199.6 | 16018.8 | 15.33322222 | 266.98 | 2x |
| RSA100 | 15390.4 | 3510.53 | 4.275111111 | 58.50883333 | 3 x |
| RSA100 | 15344.8 | 2829.9 | 4.262444444 | 47.165 | 4 x |
| RSA120 | 184096 | 30134.1 | 51.13777778 | 502.235 | 4 x |
The number field sieve algorithm has several steps. It is sieving of polynomial relations that can be paralysed amongst several machines. Following this there are several further steps which need to be performed on a single machine. These steps can be memory intensive and as the numbers got bigger took an increasing amount of time. It is for this reason that the time for factoring numbers is not directly proportional to the number of machines it is run across.
With a bit of confidence in the setup from RSA110 and RSA120 I decided to tackle the 1977 problem.
Here is the public key modulus as it appears in that article.
I logged onto to the master machine and ran the shell script which wraps a python script
./factor.sh 114381625757888867669235779976146612010218296721242362562561842935706935245733897830597123563958705058989075147599290026879543541 -t 2 -s 3 -h localhost,slave1,slave3,slave4 &> rsa129.4.out
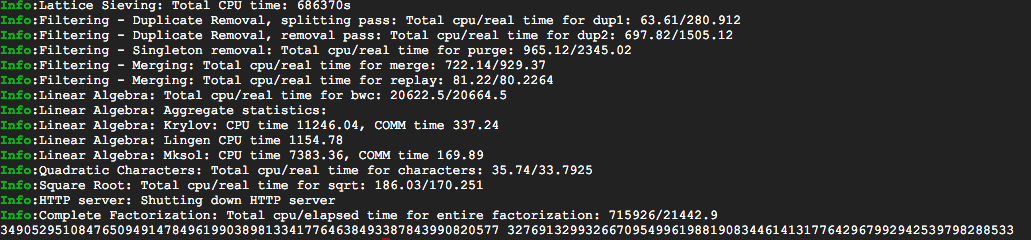
After 22 hours I checked in on it and there was both good news and bad news. The good news was that the sieving had finished! The bad news was that there had been a memory error during the next stage. It seemed quite likely that the machine had simply run out of memory as it had only 1.8GB. So I backed up the working directory of cado-nfs from /tmp and took a snapshot. I then used the snapshot to create a memory optimised machine which seemed to have similar CPUs but also 13GB of memory.
Cado-nfs makes restarting a calculation simply a matter of rerunning the original command. I dug this out of the logfile and ran it. The calculation then picked up from where it had crashed and seemed happier with more memory. After a few hours I had the answer and yes I can confirm wikipedia was correct. I'd racked up about $30 worth of usage but as I said it was in fact free due to the trial.
Once we have the factors decoding the message is easy RSA maths with the exponent being given in the article. The character encoding scheme used was also given and was a simple substitution with 0 = space and 1 = A, 2 = B etc.
I stole the modular inverse function from http://rosettacode.org/wiki/Modular_inverse#Python . Thanks to Google for the free computing. I found the cloud compute web interface to be pretty self explanatory having used AWS for a while. There are some nice features such as the usage graphs (to check always using 100% of CPUs) and a little activities pop-up which states what actions you've just taken. The in browser ssh client even seemed usable.



No comments:
Post a Comment